Swift에서 힙, 우선순위 큐 사용하기 (100% 순수 구현을 곁들인)

안녕하세요, 자료구조로 글쓰는 건 정말 오랜만입니다.

Swift에서 우선순위 큐 코드를 코테에서나, 코딩 인터뷰때 사용한다면 어떻게 할까? 부터 시작해 이글을 쓰게 되었습니다.

현재 제 주력언어는 Swift로, Heap과 관련된 서드파티 라이브러리 같은 게 있을거 같은데 코테에서나 인터뷰에선 해당 라이브러리를 쓰자니 곤란합니다. 물론 제한사항도 있을거구요. 다른 언어를 사용해도 되지만, 너무 단순한 대체법인 거 같습니다. 물론 사용해도 문제가 없고 다른 언어를 알고 있다면 상관 없겠지만요.

 

그래서 뭘 말하려고 하냐면 옛날에 큐 관련 자료를 정리 해놓고 구현해 놓았던 Heap과 우선순위 큐, 그리고 이를 사용할 수 있는 설명과 구현 코드를 제시하려 합니다.

 

[Swift 우선순위 큐 구현코드]

struct GlobalPriorityQueue<S: Equatable> {
    var compareOperator: (S, S) -> Bool
    var queue:[S]
    
    init(compareOperator: @escaping (S, S) -> Bool, queue: [S] ) {
        self.compareOperator = compareOperator
        self.queue = queue
    }
    
    private func leftChildIndex(parent index: Int) -> Int {
        return index * 2 + 1
    }
    
    private func rightChildIndex(parent index: Int) -> Int {
        return index * 2 + 2
    }
    
    private func parentIndex(child index: Int) -> Int {
        return (index - 1) / 2
    }
    
    var isEmpty: Bool {
        return queue.isEmpty
    }
    
    var count: Int {
        return queue.count
    }
    
    var pick: S? {
        return queue.first
    }
    
    mutating func enqueue(value: S) {
        queue.append(value)
        heapifyUp(from: queue.count - 1)
    }
    
    mutating func dequeue() -> S? {
        guard !queue.isEmpty else { return nil }
        
        let popedItem: S
        
        if queue.count == 1 {
            popedItem = queue.removeLast()
        } else {
            queue.swapAt(0, queue.count - 1)
            popedItem = queue.removeLast()
            heapifyDown(from: 0)
        }
        return popedItem
    }
    
    mutating func heapifyUp(from index: Int) {
        guard index > 0 else { return }
        
        let parentIndex = parentIndex(child: index)
        
        if parentIndex >= 0 && compareOperator(queue[index], queue[parentIndex])  {
            queue.swapAt(parentIndex, index)
            heapifyUp(from: parentIndex)
        }
    }
    
    mutating func heapifyDown(from index: Int) {
        let leftChildIndex = leftChildIndex(parent: index)
        let rightChildIndex = rightChildIndex(parent: index)
        var highestPriorityIndex = index
        
        if leftChildIndex < queue.count && compareOperator(queue[leftChildIndex], queue[highestPriorityIndex]) {
            highestPriorityIndex = leftChildIndex
        }
        
        if rightChildIndex < queue.count && compareOperator(queue[rightChildIndex], queue[highestPriorityIndex]) {
            highestPriorityIndex = rightChildIndex
        }
        
        if highestPriorityIndex != index {
            queue.swapAt(index, highestPriorityIndex)
            heapifyDown(from: highestPriorityIndex)
        }
    }
    
}

 

[힙]

완전이진트리(부모노드에 자식 노드를 최대 2개로 제한)한 트리에서 가장크거나(최대힙) 작은(최소힙) 값을 O(1)시간에 값을 추출하기 위해 사용되는 트리형태의 자료구조입니다.

• 내부 동작으로 인해 값이 추출되거나 삽입 되면, O(Log N) 시간 복잡도가 소요되는 자료구조로 우선순위 큐의 기반이 되는 자료구조입니다.
• 힙은 배열의 인덱스 관계로도 표현이 가능합니다.(완전 이진트리 형태이기 때문)
  • 예를들어 인덱스가 0부터 시작한다면, 부모 0의 자식노드 인덱스는 1,2가 되겠죠. 이런 관계를 소스코드에선 leftChild, rightChild, parent 메소드로 구현해 놓았습니다.

[삽입]

힙에서 삽입은 다음과 같습니다. (소스코드에서 enqueue 메소드입니다.)

트리에 가장 끝 자리에 삽입하고, 부모 노드와 비교해 우선순위가 높다면 swap하는 방식입니다.

이러한 동작은 부모노드가 자식노드보다 우선순위가 높게 될때까지 반복하게 됩니다. -> heapifyUp 연산

소스코드 상에서 enqueue 메소드 내부에  heapifyUp 연산으로 구현한 동작이 위 설명입니다.

[ 삭제]

힙의서 삭제는 다음과 같은 그림입니다. (소스코드에서 dequeue)

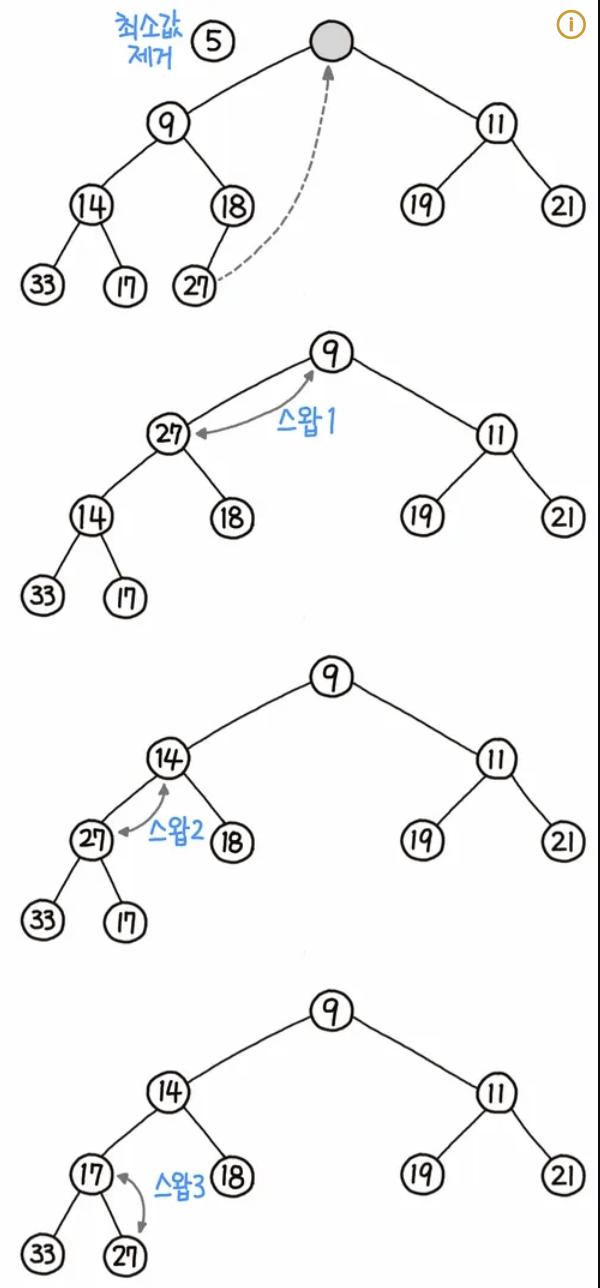
힙에서 값 제거란, 가장 우선순위가 높은 값을 제거한다는 뜻입니다. 그래서 힙 구조상 최상위 루트 노드를 추출하고 힙 자료구조에 맞게 다시 재구성이 필요합니다. 이러한 연산을 HeapifyDown이라 합니다. 

• 최상위 루트 노드 추출후 힙 구조에서 가장 마지막 노드(인덱스가 가장 큰) 노드를 최상위 노드로 위치시킵니다.
• 부모와 자식 노드를 비교해 교체한다.
• 힙의 구조를 만족할 때 까지 부모와 자식 노드를 비교해 교체한다.

[우선순위 큐]

FIFO로 우선순위가 높은 순서부터 값을 반환합니다. 보통 Heap 자료구조를 활용합니다. 메커니즘은 Heap기반이니 메커니즘 설명은 생략하겠습니다. 위 소스 코드의 예제에서 enqueue, dequeue 메소드에 해당합니다. 

소스코드를 보면 Gemeric이 Equatable이므로 원시타입을 대입하시거나 별도로 해당 프로토콜을 구현해서 사용하시면 됩니다.

 

[References]

힙 트리